Illustrator詳細解析鋼筆工具的使用技巧(2)
文章來源于 站酷,感謝作者 靈動思維 給我們帶來經精彩的文章!仔細看一下這兩個方向線
再這樣想象:
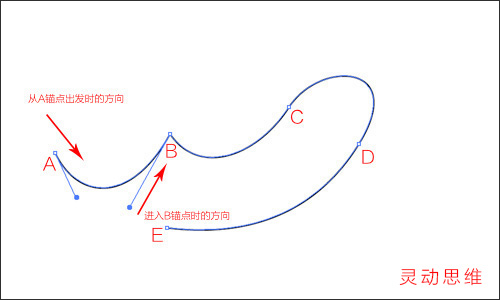
一個人要從A點到B點,在A點出發的時候,位于A點的其他人看到他是朝著上偏右的方向走的,而位于B點的人,看到他是朝著下偏左的方向來的。
那么綜合兩地的觀測結果。就可以得出這個人行走的路線:必定是一個類似拋物線的弧形
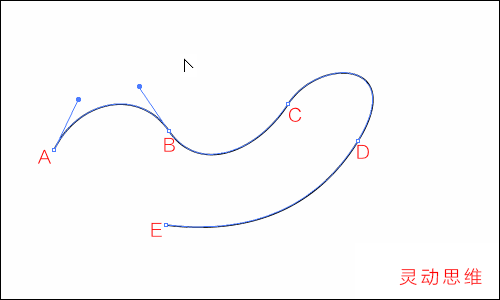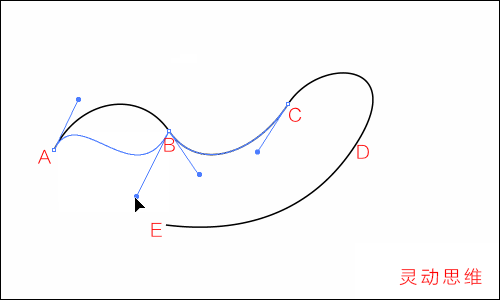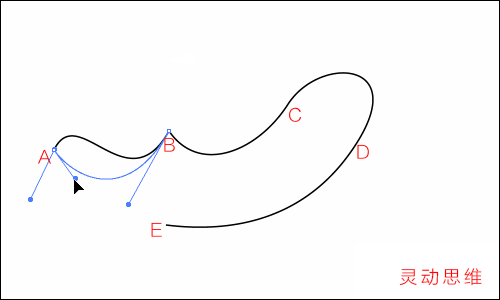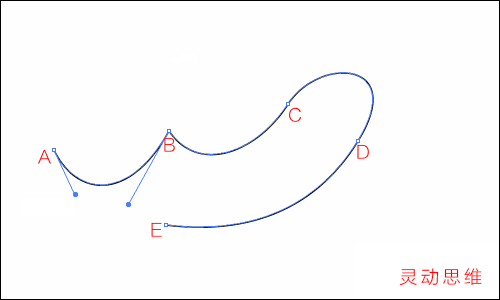
現在我們選擇如圖的“錨點工具”,該工具用來修改方向線
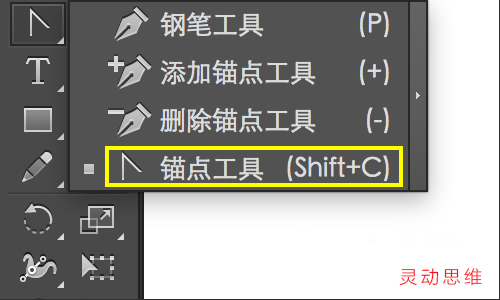
然后如下圖所示般改變AB錨點上的方向線,將會看到曲線彎曲度的改變
注意方向線末端有一個小圓點,這個圓點稱為“手柄”,要點擊手柄拖動才可以改變方向線
結合剛才所作的比喻,就不難理解了:
1 修改B錨點方向線為下,相當于指定那個人從A點上方出發后,從B點下方進入,那么所走的路程就是一個S形
2 再修改A錨點方向線為下,相當于從A點下方出發,再從B點下方進入,所走的就是一個下弧形的路程
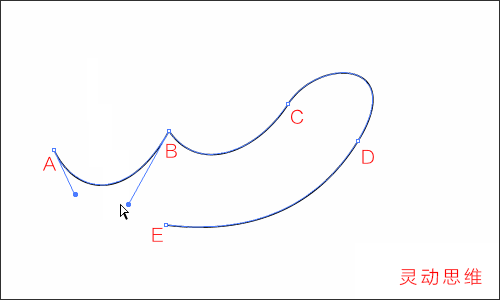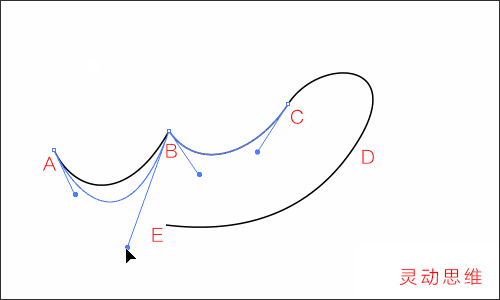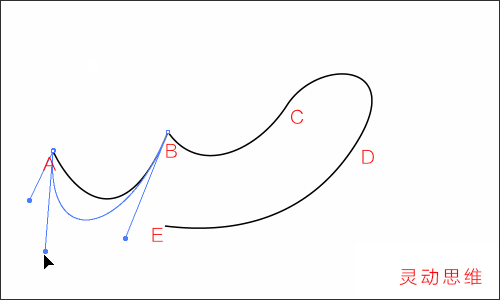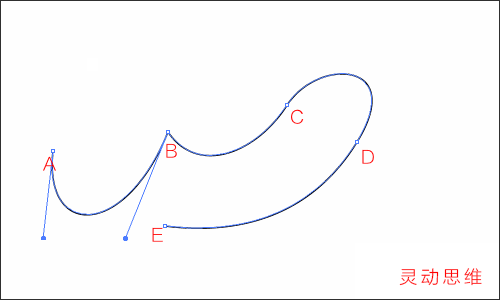
修改后的方向線如下圖:
明白了方向線的方向對曲線形態的影響后,我們來看一下方向線長短造成的影響
如下圖般,在同一方向上拖拉方向線:(可使用“直接選擇工具”)
對于一個錨點而言,如果方向線越長,那么曲線在這個方向上走的路程就越長,反之就越短
可以這樣設想,曲線是一個橡皮筋,在頭尾兩端有兩個力在各自的方向上拉,哪個方向上力氣大,則橡皮筋就朝
向這個方向多靠攏一些。反而反之
除了修改錨點之外,也可以利用“直接選擇工具”,在片斷上修改曲線的形態,如下圖:
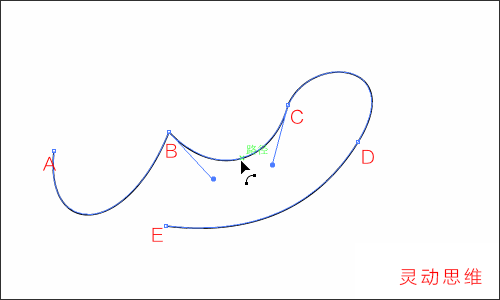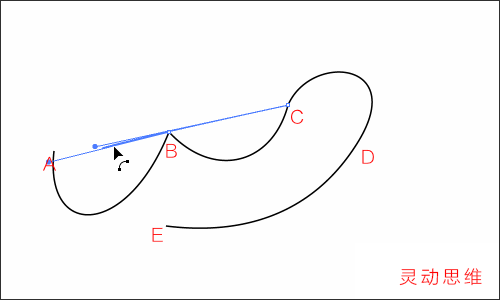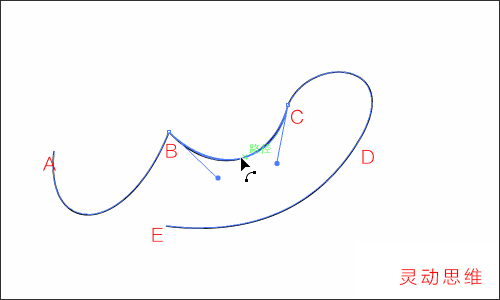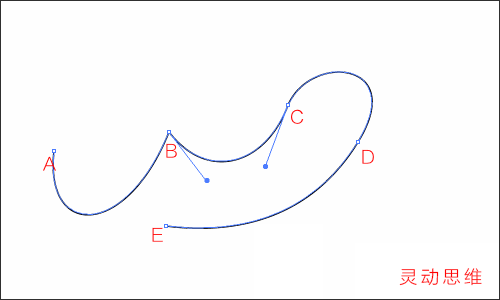
注意:這并不能說是“修改了片斷”,而應該說是“同時修改了兩個錨點”
牢記原則:路徑的片斷是由錨點組成的,只有修改錨點才能改變片斷形態,這是不可逆的因果關系
小結:
對于這條曲線上的除了起點和終點的AE兩個錨點而言,都存在兩條方向線:
一條是從上一個錨點“來向”的方向線;另一條是通往下一個錨點的“去向”的方向線,
對于起點,只存在“去向”的方向線;對于終點,只存在“來向”的方向線
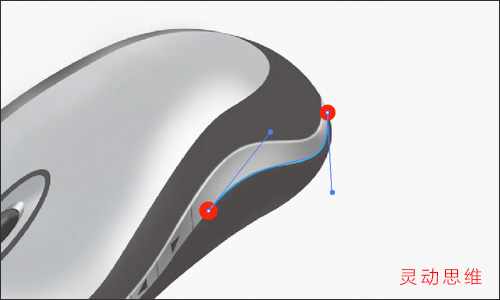
下面讓我們做個小練習,如圖:

現在要求在兩個紅點之間繪制一條緊貼鼠標外廓的曲線,很可能你們繪制出來的是如下圖這個樣子的

雖然要求是達到了,但是這樣的路徑上使用了3個錨點。再看下圖:
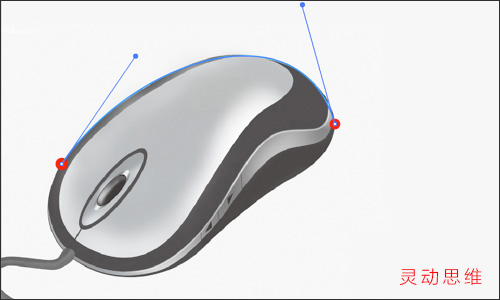
同樣的曲線效果,這里只用了兩個錨點來繪制
移動兩個紅點的位置再行繪制,很可能你們繪制的效果是這樣:
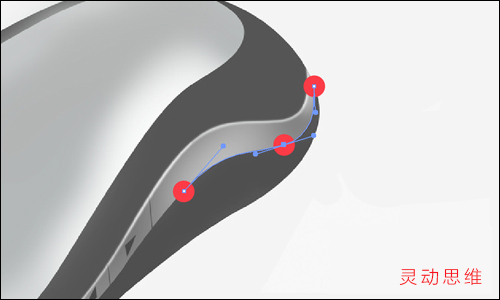
而實際上呢,也只需要用兩個錨點就可以繪制這條曲線了,如下圖
 情非得已
情非得已
-
 Illustrator繪制扁平化風格的建筑圖2020-03-19
Illustrator繪制扁平化風格的建筑圖2020-03-19
-
 Illustrator制作扁平化風格的電視機2020-03-18
Illustrator制作扁平化風格的電視機2020-03-18
-
 Illustrator繪制漸變風格的建筑場景插畫2020-03-12
Illustrator繪制漸變風格的建筑場景插畫2020-03-12
-
 佩奇插畫:用AI繪制卡通風格的小豬佩奇2019-02-26
佩奇插畫:用AI繪制卡通風格的小豬佩奇2019-02-26
-
 插畫設計:AI繪制復古風格的宇航員海報2019-01-24
插畫設計:AI繪制復古風格的宇航員海報2019-01-24
-
 房屋插畫:AI繪制圣誕節主題的房屋插畫2019-01-21
房屋插畫:AI繪制圣誕節主題的房屋插畫2019-01-21
-
 圣誕插畫:AI繪制簡約風格圣誕節插畫2019-01-21
圣誕插畫:AI繪制簡約風格圣誕節插畫2019-01-21
-
 燈塔繪制:AI繪制的燈塔插畫2019-01-21
燈塔繪制:AI繪制的燈塔插畫2019-01-21
-
 時尚船錨:AI繪制鮮花裝飾的船錨圖標2019-01-18
時尚船錨:AI繪制鮮花裝飾的船錨圖標2019-01-18
-
 扁平寶箱圖形:AI繪制游戲中常見的寶箱2019-01-18
扁平寶箱圖形:AI繪制游戲中常見的寶箱2019-01-18
-
 Illustrator制作復古風格的郵票效果2021-03-10
Illustrator制作復古風格的郵票效果2021-03-10
-
 Illustrator制作扁平化風格的電視機
相關文章5132020-03-18
Illustrator制作扁平化風格的電視機
相關文章5132020-03-18
-
 Illustrator繪制漸變風格的建筑場景插畫
相關文章2072020-03-12
Illustrator繪制漸變風格的建筑場景插畫
相關文章2072020-03-12
-
 詳細解析AI快速繪制角度漸變
相關文章6362019-08-29
詳細解析AI快速繪制角度漸變
相關文章6362019-08-29
-
 餅圖工具:用AI制作立體圖形教程
相關文章17832019-03-26
餅圖工具:用AI制作立體圖形教程
相關文章17832019-03-26
-
 字母海報:用AI制作翻頁風格海報教程
相關文章13652019-03-19
字母海報:用AI制作翻頁風格海報教程
相關文章13652019-03-19
-
 2.5D插畫:用AI繪制2.5D風格剪紙插畫
相關文章8432019-03-08
2.5D插畫:用AI繪制2.5D風格剪紙插畫
相關文章8432019-03-08
-
 佩奇插畫:用AI繪制卡通風格的小豬佩奇
相關文章11492019-02-26
佩奇插畫:用AI繪制卡通風格的小豬佩奇
相關文章11492019-02-26
-
 矢量插畫:使用AI制作滑板車插畫教程
相關文章6612019-02-26
矢量插畫:使用AI制作滑板車插畫教程
相關文章6612019-02-26
